⇒ 「3点を通る円」と「2点とある直線上に中心がある円」の方程式の求め方 いろいろな解法が思い浮かぶのは、図やグラフを書いているからですよ。 ⇒ 図形と方程式の要点 単元毎のまとめですが全体を見渡しておく方が理解しやすいです。円と直線の位置関係 円と直線の位置関係は 異なる2点で交わる 1点で接する 共有点を持たない のいずれか。 円と直線の関係の判定方法 円の中心から直線までの距離と円の半径を比較して判定する。 (点と直線の3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円の半径
3点から円の中心と半径を求める Satoh
円 中心 求め方 3点
円 中心 求め方 3点-通る $3$ 点が決まれば円は一つに定まるので、その方程式を求めてあげれば自然と中心がわかる、という仕組みになっております。 ここでは、一番わかりやすい解法で解いていきたいと思います♪Tubokura08さんの御回答と同じことなのですが。m(__)m 円周上に3点をとり、三角形を描きます。 (三角形は、正三角形に近い方が描きやすいかもしれません。) (目分量で十分です。) 2辺の垂直2等分線の交点が、円の中心Cになりますね。



高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット
Tubokura08さんの御回答と同じことなのですが。m(__)m 円周上に3点をとり、三角形を描きます。 (三角形は、正三角形に近い方が描きやすいかもしれません。) (目分量で十分です。) 2辺の垂直2等分線の交点が、円の中心Cになりますね。4 円弧3点の座標から円の中心座標と半径の求め方をお願いいたします。 5 この図のpとqの座標と右上の円の中心の座標の求め方を教えていただきたいです。どちらの円も半径5です。一直線上にない任意の3点が与えられれば、その3点を通る円を求めることができます。 ここでは、任意の3点を通る円の中心座標と半径を求める方法を2種類の方法で紹介します。 なお、以下では、円の方程式を、 とし、点が円の中心点の座標、が半径とします。
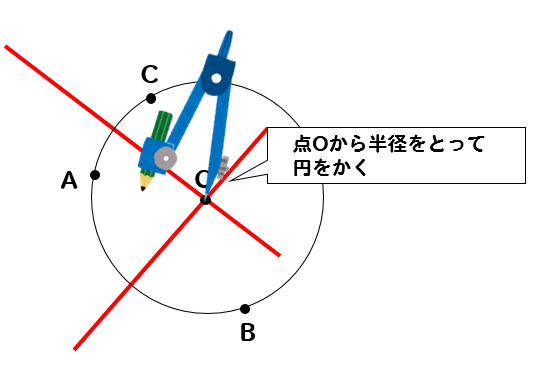
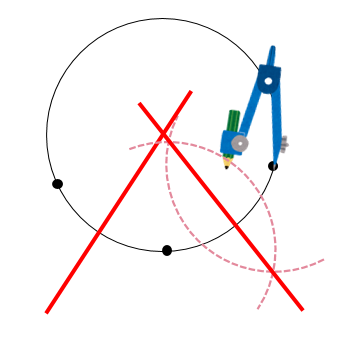
それぞれの意味や求め方を詳しく説明していくので、ぜひこの記事を通してマスターしてくださいね! 内接円の中心 ちなみに、この \(3\) 点は点 \((2,3)\) を中心とした半径 \(5\) の円を表す方程式なのです。つまり \(x^2y^2lxmyn=0\) (\(l,m,n\) は整数) であれば 円の方程式 なのではないかと思われます。もともと円であるとわかっている式を展開したらこのような形が出てきたのですから。まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 そして、円周上の3点 中学数学扇形の中心角の求め方3パターンピザでわかる
三点を通る円の中心座標と半径を求める公式を教えてください。ちなみに3点はa(-4,3) b(5,8) c(2,7) です。高校の頃にやった覚えがあるのですが、現在大学4年になりまして、すっかり忘れてしまいました。どなたか知っている方がいらTubokura08さんの御回答と同じことなのですが。m(__)m 円周上に3点をとり、三角形を描きます。 (三角形は、正三角形に近い方が描きやすいかもしれません。) (目分量で十分です。) 2辺の垂直2等分線の交点が、円の中心Cになりますね。3母点の接点円の中心の求め方 母点p1、p2及びp2、p3の垂直2等分線をy1=a1x1+c1 y2=a2x2+c2とする それぞれの垂直2等分線の傾きを a1=-(x2-x1)/(y2-y1) a2=-(x3-x2)/(y3-y2)とする



中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室


円周上の3点から円の中心を求める
求め方 3点を通る円の中心は、その三点を頂点とする三角形の外心となる。 (求める円はその三点を頂点とする三角形の外接円) 三角形の各辺の垂直二等分線の交点がその三角形の外心となる。 外心は3つの頂点から等距離にある。 その外心から各点の頂点の距離が円の半径となる。 外心の求め方円の方程式とは? 円の方程式とは、 中心の座標と円の半径を用いて、円を方程式で表したもの です。 表し方には「基本形」と「一般形」の \(2\) 通りがあります。 基本形の公式 円の方程式を基本形で表現すると、円の中心と半径が一目でわかります。関数 2乗に比例する関数の変域の考え方 平面図形 おうぎ形の中心角 平面図形 二等分線の作図のしかた 平面図形 垂直二等分線の作図のコツ 平面図形 3辺から等しい距離にある点の求め方 平面図形 円の中心を求める作図



中学数学 三平方の定理 円錐 のポイントと練習問題


中1 作図 円の中心を求める方法を解説 数スタ
三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa=ob=oc ol⊥bc 、 om⊥ac 、 on⊥ab4 円弧3点の座標から円の中心座標と半径の求め方をお願いいたします。 5 この図のpとqの座標と右上の円の中心の座標の求め方を教えていただきたいです。どちらの円も半径5です。Ptは3点 a , b , t を通る円の 点tでの接線 // 以上、円に関する性質でした! これらの「武器」と次の過程で学ぶ「三平方の定理」があれば 中学数学の円に関する問題で解けないものはないですね! お疲れ様でした! その他の問題は、「問題集」で !!



中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室



円周角と孤の比 中学数学に関する質問 勉強質問サイト
は点 \((2,3)\) を中心とした半径 \(5\) の円を表す方程式なのです。つまり \(x^2y^2lxmyn=0\) (\(l,m,n\) は整数) であれば 円の方程式 なのではないかと思われます。もともと円であるとわかっている式を展開したらこのような形が出てきたのですから。Ptは3点 a , b , t を通る円の 点tでの接線 // 以上、円に関する性質でした! これらの「武器」と次の過程で学ぶ「三平方の定理」があれば 中学数学の円に関する問題で解けないものはないですね! お疲れ様でした! その他の問題は、「問題集」で !!一直線上にない任意の3点が与えられれば、その3点を通る円を求めることができます。 ここでは、任意の3点を通る円の中心座標と半径を求める方法を2種類の方法で紹介します。 なお、以下では、円の方程式を、 とし、点が円の中心点の座標、が半径とします。



標準 3点を通る円の作図 なかけんの数学ノート



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
Tubokura08さんの御回答と同じことなのですが。m(__)m 円周上に3点をとり、三角形を描きます。 (三角形は、正三角形に近い方が描きやすいかもしれません。) (目分量で十分です。) 2辺の垂直2等分線の交点が、円の中心Cになりますね。一直線上にない任意の3点が与えられれば、その3点を通る円を求めることができます。 ここでは、任意の3点を通る円の中心座標と半径を求める方法を2種類の方法で紹介します。 なお、以下では、円の方程式を、 とし、点が円の中心点の座標、が半径とします。まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 そして、円周上の3点 中学数学扇形の中心角の求め方3パターンピザでわかる



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
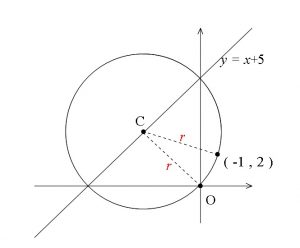


3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方
(a,b)(c,d)(e,f)を通る式x^2y^2lxmyn=0のl,m,nと円の中心点の座標及び半径を求めます 指定した3点を通る円の式 高精度計算サイト ゲストさんまずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 そして、円周上の3点 中学数学扇形の中心角の求め方3パターンピザでわかるPtは3点 a , b , t を通る円の 点tでの接線 // 以上、円に関する性質でした! これらの「武器」と次の過程で学ぶ「三平方の定理」があれば 中学数学の円に関する問題で解けないものはないですね! お疲れ様でした! その他の問題は、「問題集」で !!
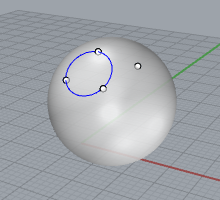


球の中心の求め方 Inak Engineering Llc



高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット
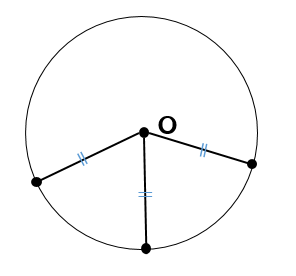
右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B)平面で定義された曲線 上の点 p から曲線に沿って だけ変位した点を q とする.この 部分を円弧とみなし,円の中心を点 c ,角pcqを とすると,この円の半径は である(絶対値をとっているのは角 が時計回りの場合,負の値となるからである).ここで,極限 をとると,点 p における曲率半径中心がOである円を円Oと呼ぶ。円Oにおいて、円周上の2点A , Bをとったとき、AからBまでの円周の部分を 弧AB (こAB)といい、 と書く。 ∠ を弧ABに対する 中心角(ちゅうしんかく、英:central angle) という。 また、弧ABを中心角 ∠ に対する弧(こ、英:arc)という。


コンパスと定規を使った正三角形の描き方 図形の描き方011a 夏貸文庫


二次元図形における円周上の座標 X Y を求める方法を教えてくだ Yahoo 知恵袋
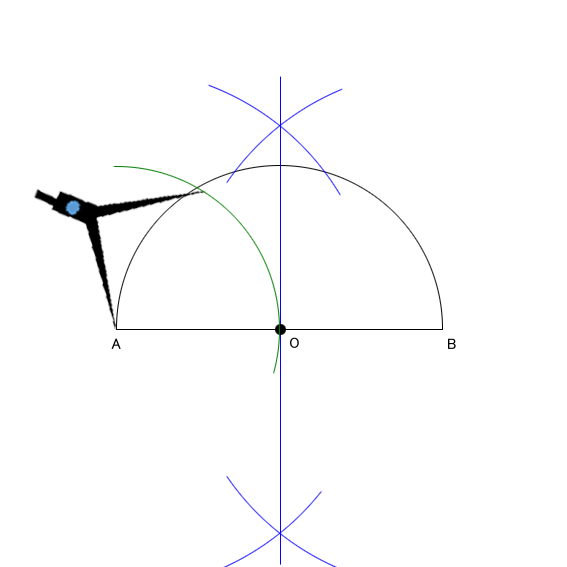
円とは、円の中心Oから等距離にある点の集合です。 中心Oの求め方 ではまず、点A、点Bから等しい距離にある点を求めてみましょう。 先ほど示した垂直2等分線を使います。 ABを垂直に2等分する線abは、上の図のようになります。⇒ 「3点を通る円」と「2点とある直線上に中心がある円」の方程式の求め方 いろいろな解法が思い浮かぶのは、図やグラフを書いているからですよ。 ⇒ 図形と方程式の要点 単元毎のまとめですが全体を見渡しておく方が理解しやすいです。



垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア


外接円 外心について



3つの円がなす角の中心座標方程式を求め方を教えてください 3つの円が 数学 教えて Goo



円 数学 Wikipedia



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
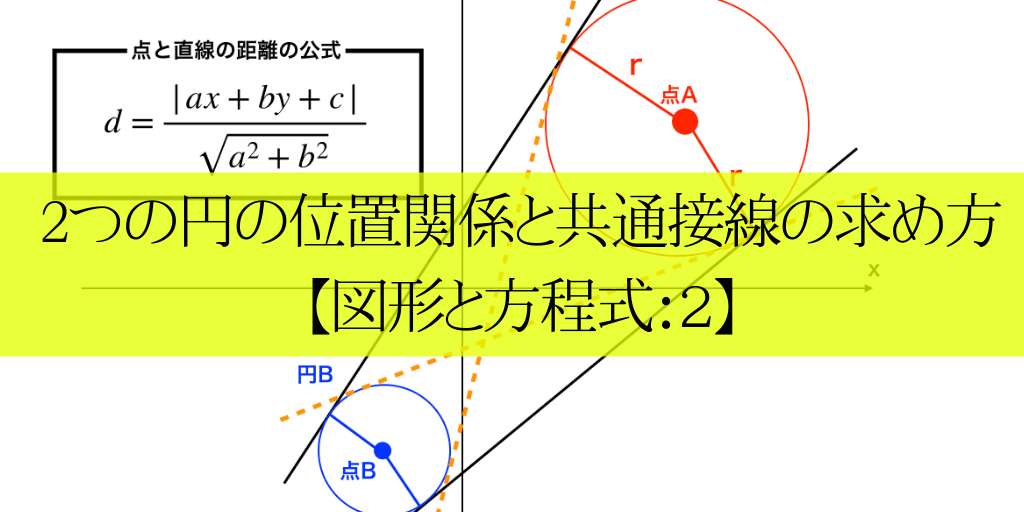


2つの円の位置関係と共通接線の求め方 図形と方程式 2



外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ


3点から円の中心と半径を求める Satoh



外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



3 3pになる求め方教えていただきたいです Clear
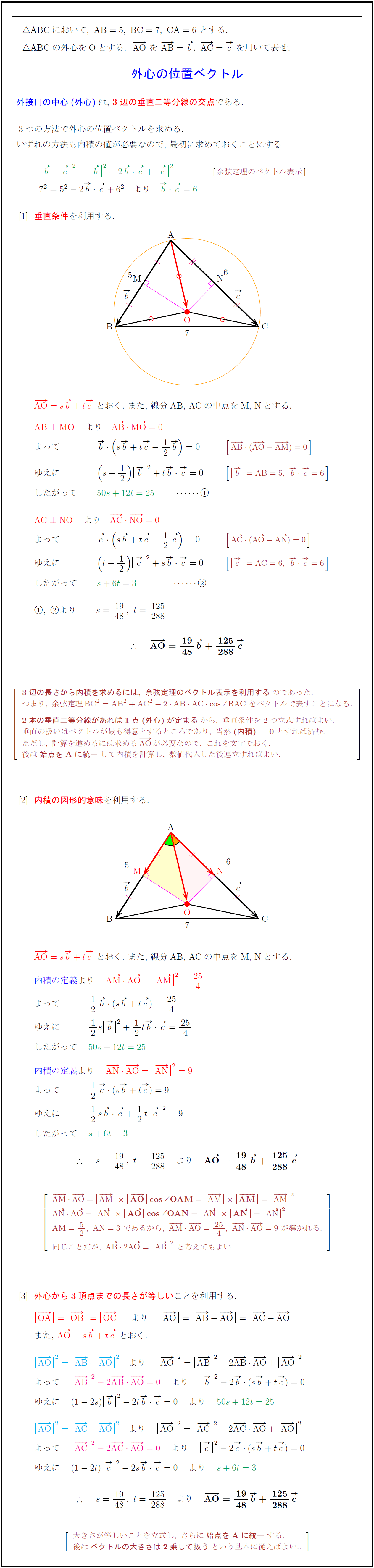


高校数学b 三角形の外心の位置ベクトル 受験の月


中学数学教えてください 図のように 点oを中心とする円の周上に3点a Yahoo 知恵袋


3次元空間での円の中心の求め方 Inak Engineering Llc


3点の座標から簡単に角度と回転方向を求める 2 3 N次元 外積を用いる方法


中1 作図 円の中心を求める方法を解説 数スタ



3つの円がなす角の中心座標方程式を求め方を教えてください 3つの円が 数学 教えて Goo


内接円 内心



質問 数学a 図形 三角形に外接円が必ず存在する理由 オンライン無料塾 ターンナップ


3点から円の中心と半径を求める Satoh


外接円 外心について
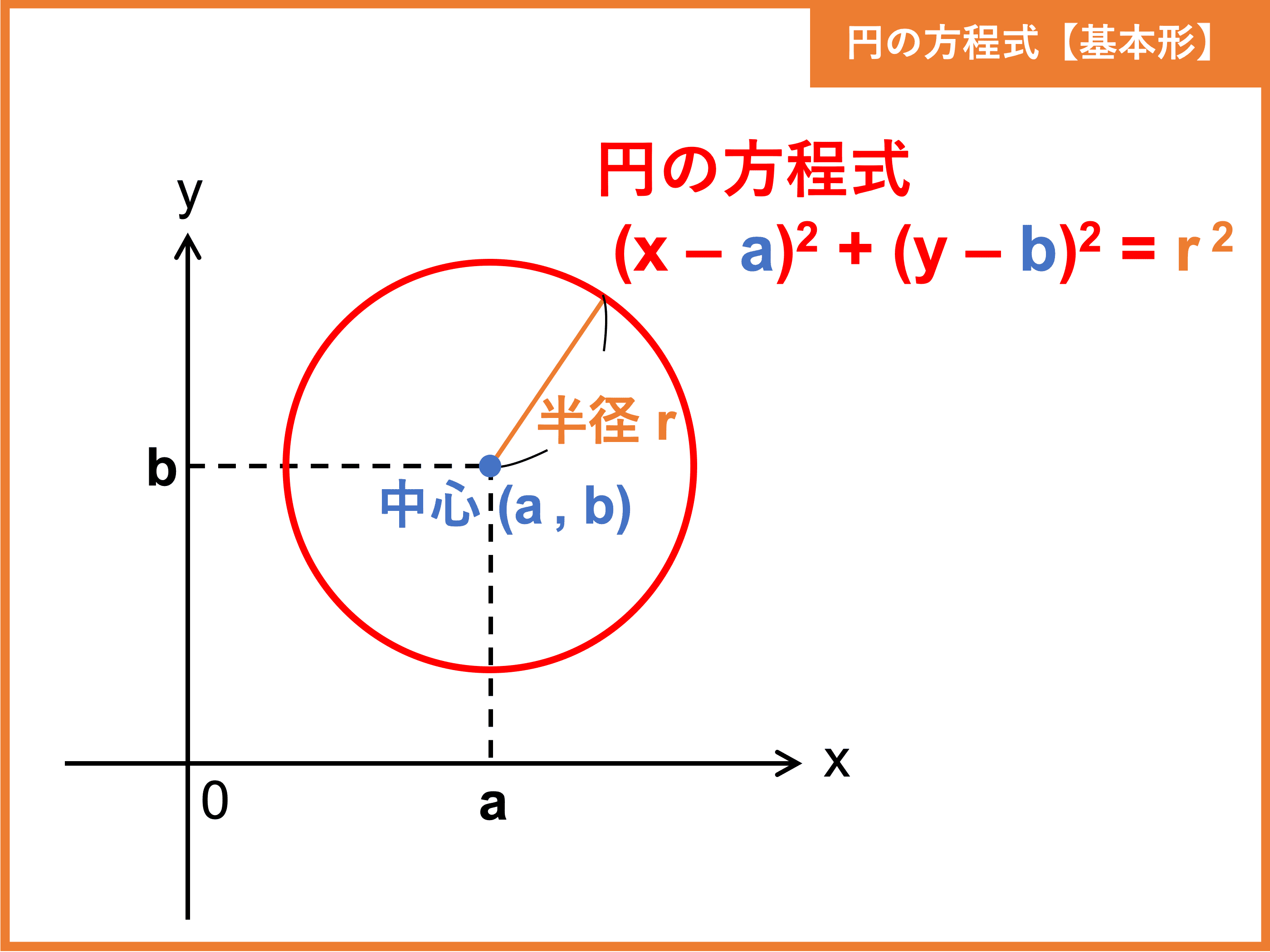


円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典


無料印刷可能な画像 最高 50 円 中心 求め方 作図
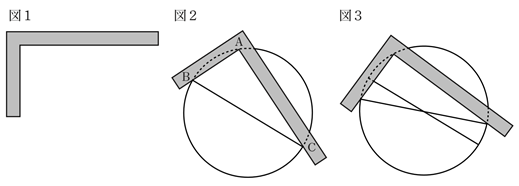


曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級
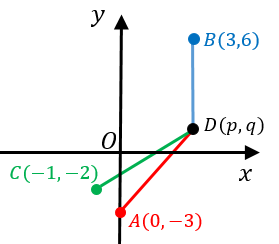


3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
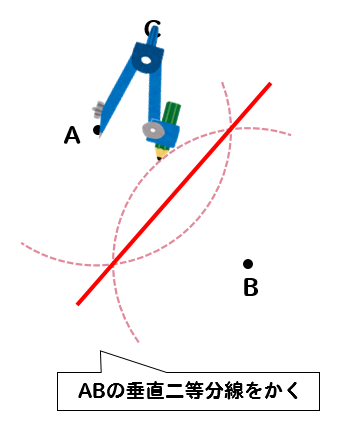


中1 作図 円の中心を求める方法を解説 数スタ
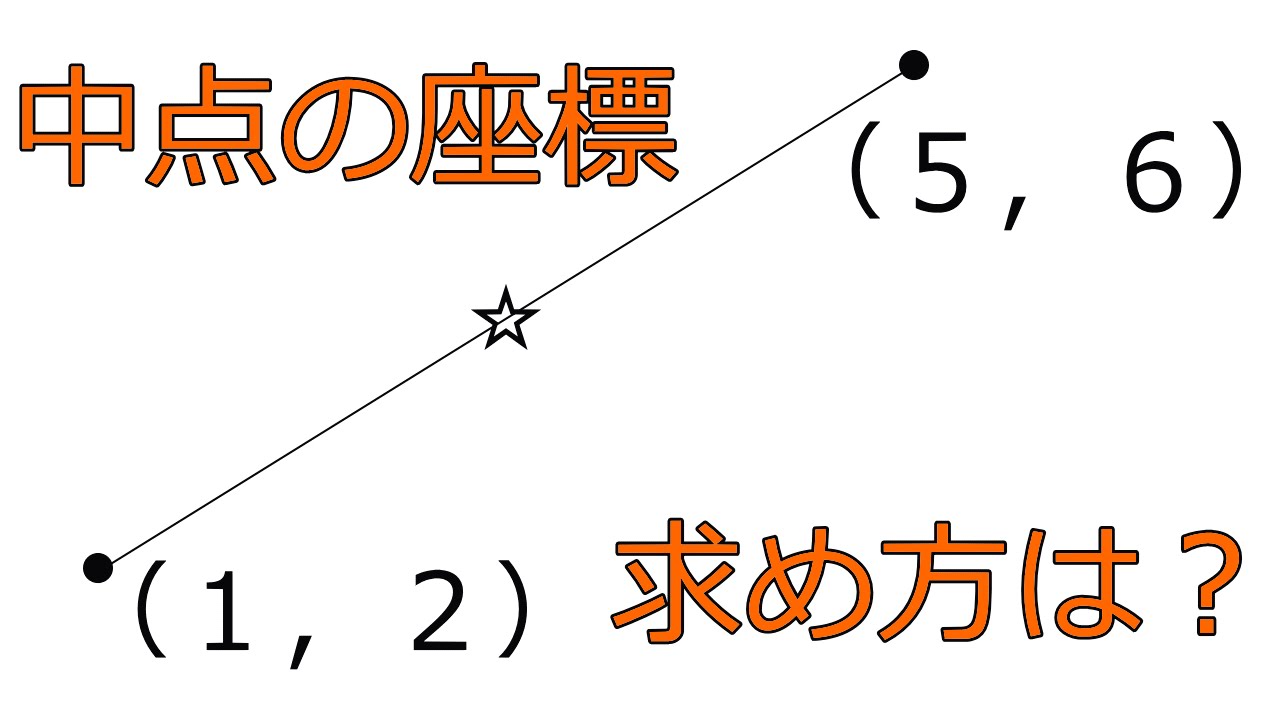


中点の座標の求め方 中学1年数学 Youtube



垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
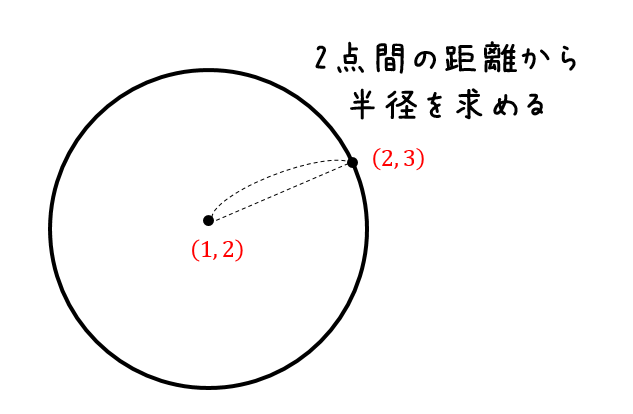


円の方程式の求め方まとめ パターン別に解説するよ 数スタ
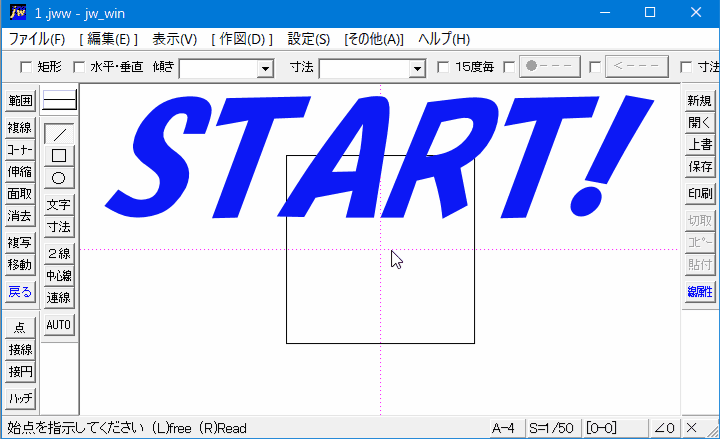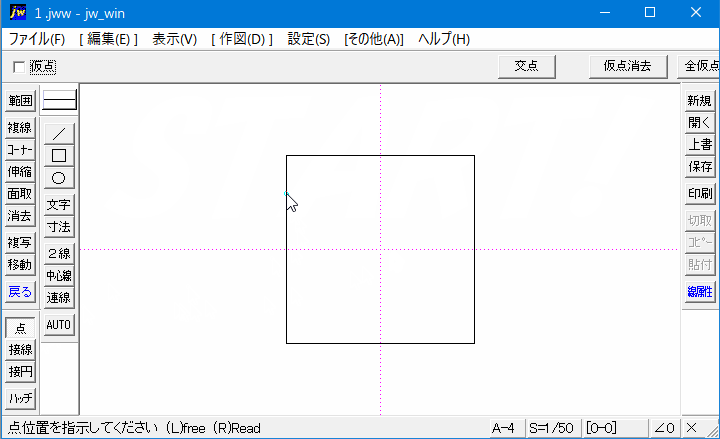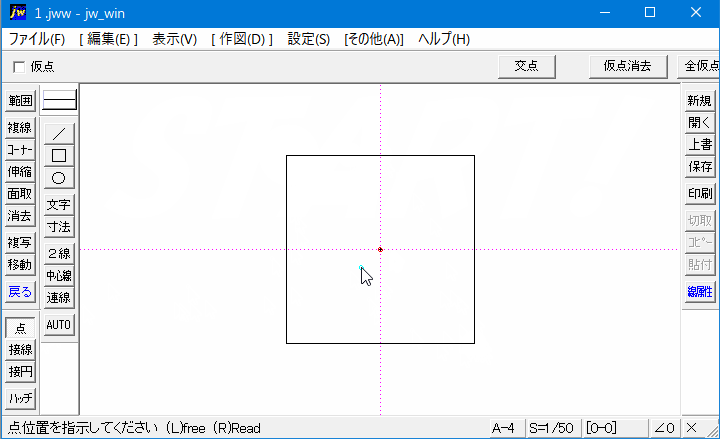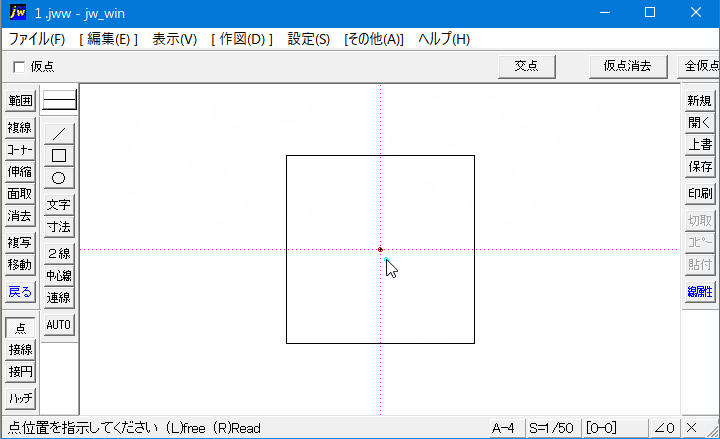


Jwcad 矩形の中心点の出し方



2 の解説3行目までは理解できました 5行目でいきなり求め 高校数学に関する質問 勉強質問サイト


3次元空間での円の中心座標の求め方についてご教授ください3次元空間で Yahoo 知恵袋
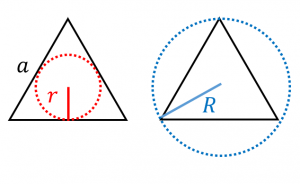


正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学
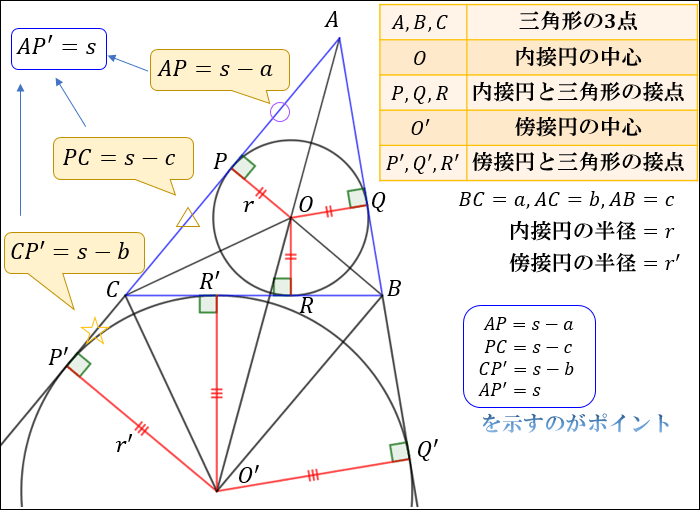


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
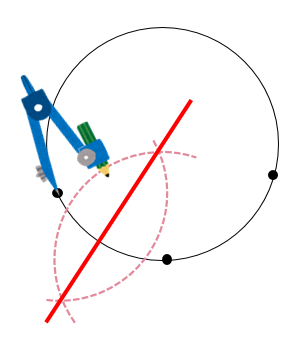


中1 作図 円の中心を求める方法を解説 数スタ



円上を動く点で定まる軌跡 高校数学に関する質問 勉強質問サイト



高校数学 3点を通る円の方程式の決定 練習編 映像授業のtry It トライイット
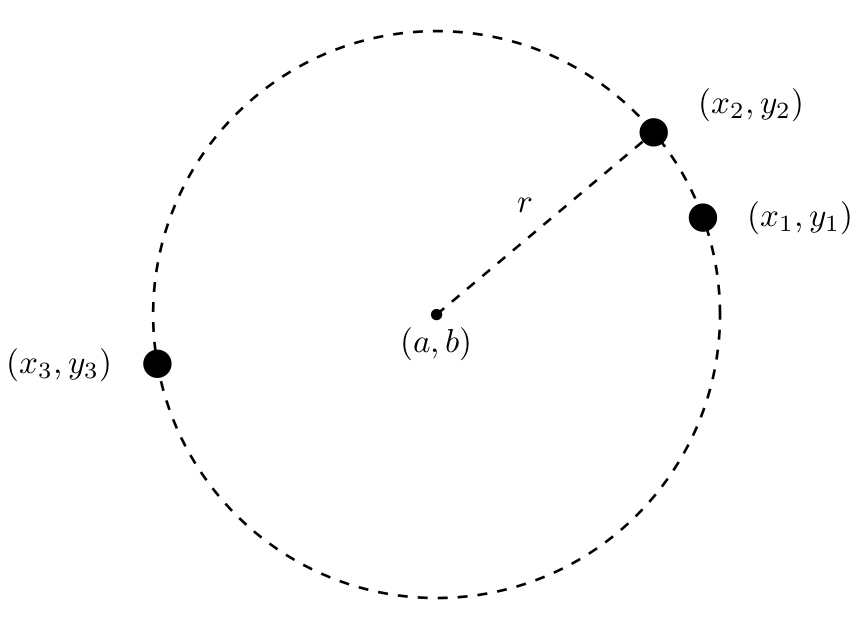


3点を通る円の中心と半径 Notes Jp



3点を通る円 の作図方法 コンパス 定規 数学fun



接点bの座標の求め方を教えてください お願いします Clear



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
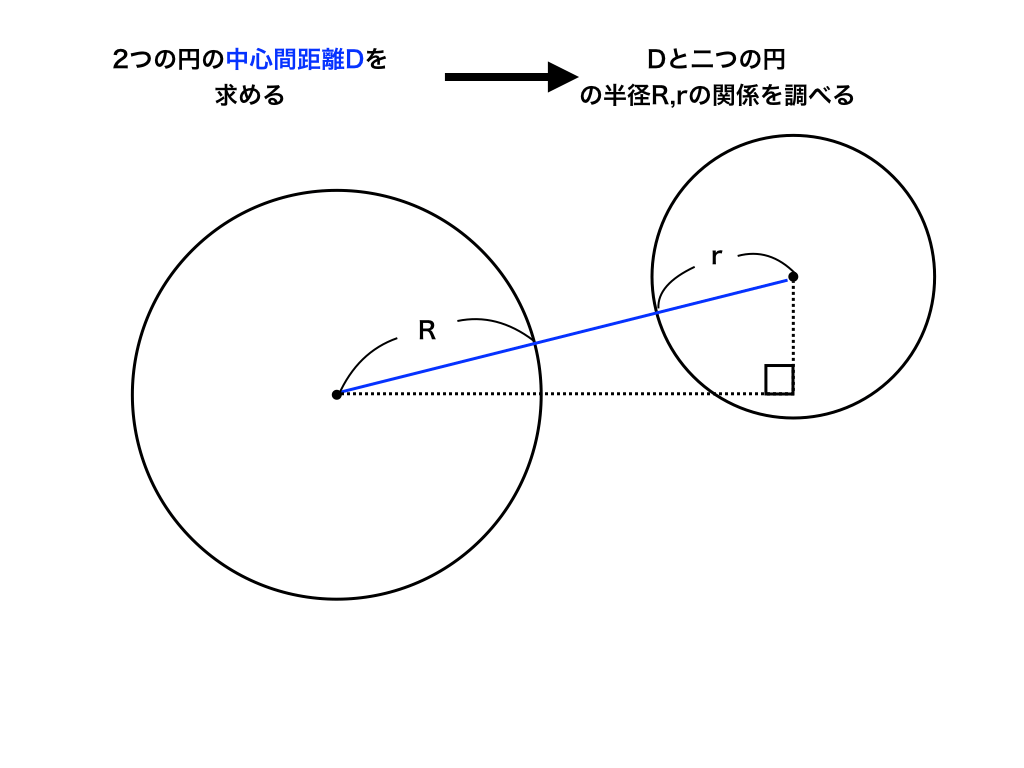


2つの円の位置関係と共通接線の求め方 図形と方程式 2


3点を通る円の方程式を求める方法



3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ


Studydoctorさまざまな円の方程式の求め方 高校数学 Studydoctor



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
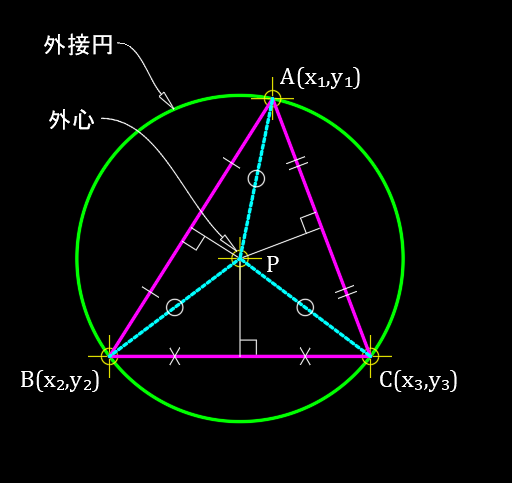


3点を通る円を求める Qiita


コンパスと定規を使った渦巻き線 アルキメデスの螺旋 の描き方 図形の描き方022a 夏貸文庫


幾何計算 2点と半径から円の中心点を求めます Satoh



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
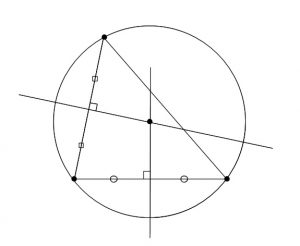


3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
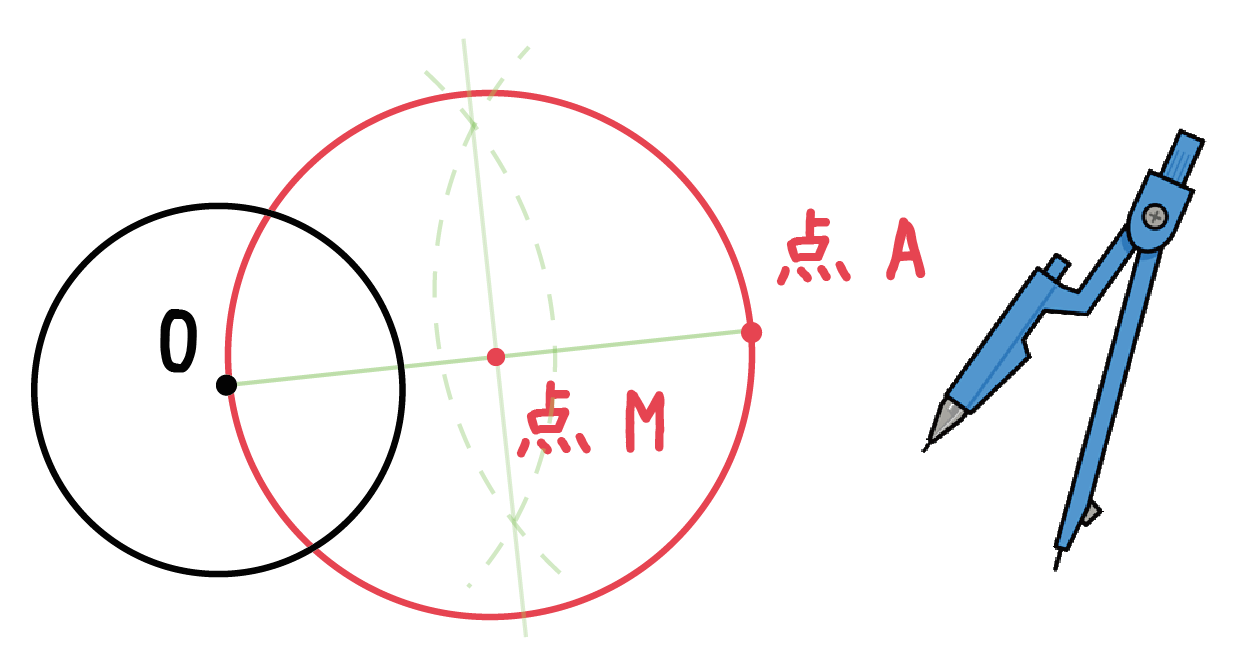


中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく
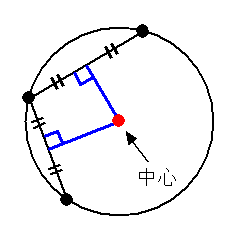


3次元空間での円の中心の求め方 Inak Engineering Llc
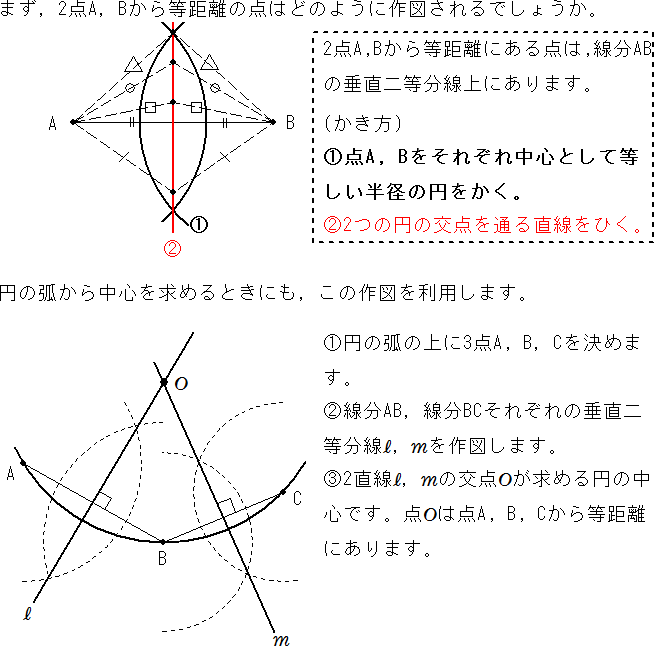


平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト


3点が与えられている三角形の外心の座標の求め方を教えて下さい Yahoo 知恵袋
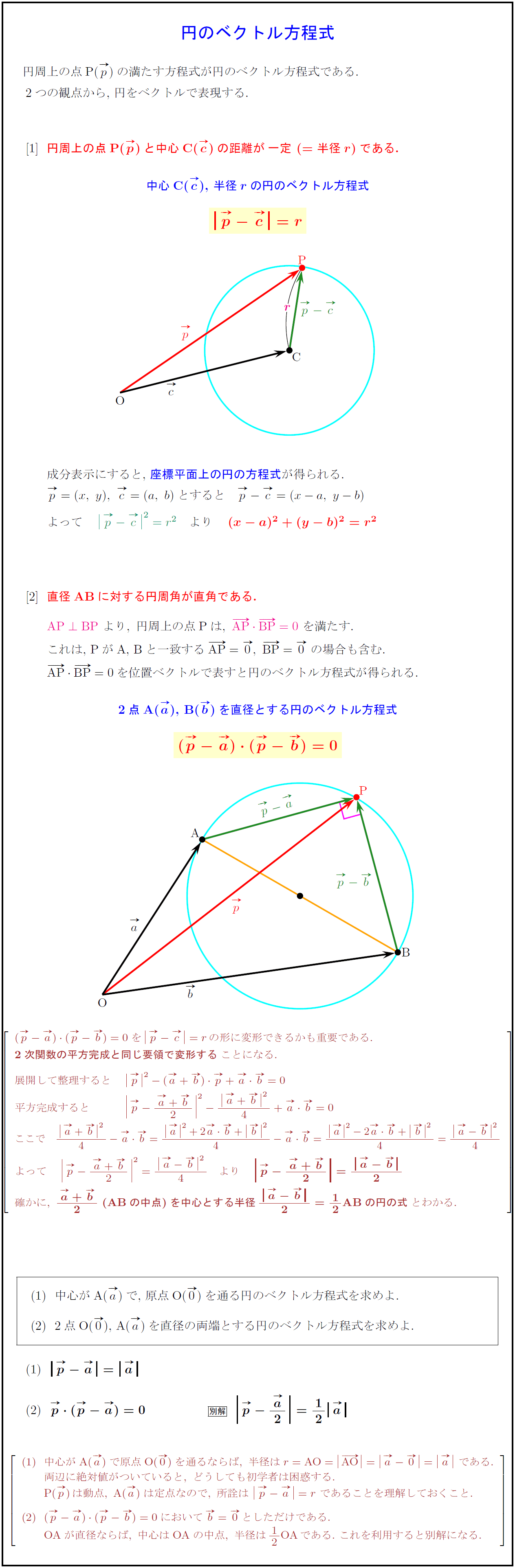


高校数学b 円のベクトル方程式2パターン 受験の月


3点から円の中心と半径を求める Satoh



三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア


中1 作図 円の中心を求める方法を解説 数スタ


九点円の定理 思考力を鍛える数学



円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



です 中心の求め方についてですが Clear
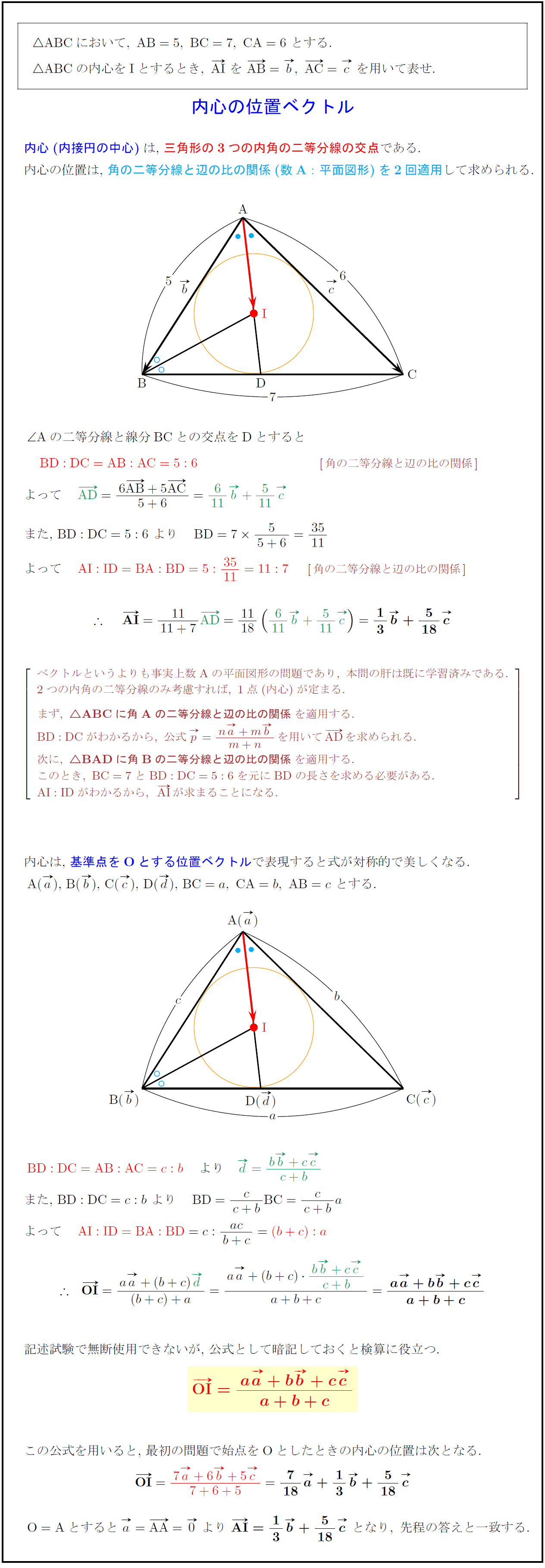


高校数学b 三角形の内心の位置ベクトル 受験の月



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



三角形の内接円の方程式の求め方 数学の偏差値を上げて合格を目指す



中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
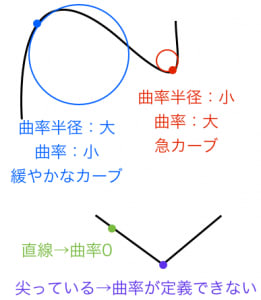


曲率 曲率半径の感覚的な意味と求め方 高校数学の美しい物語


円の描き方 円 パースフリークス
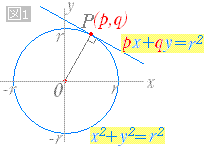


円の接線の方程式
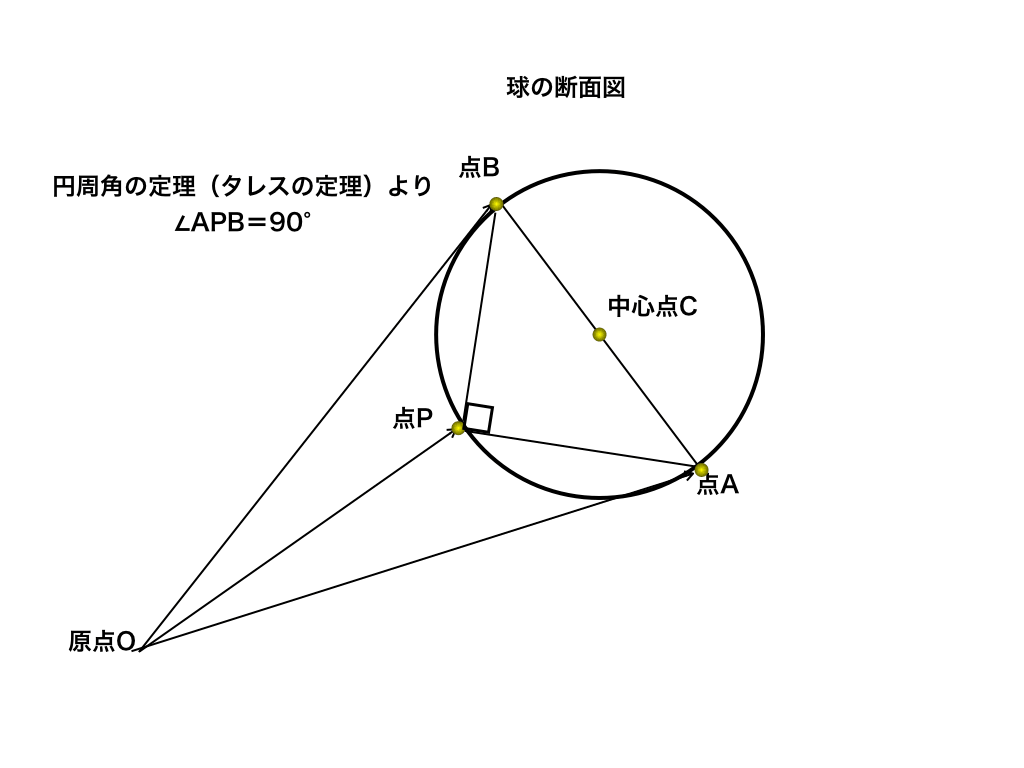


球面の方程式の求め方と問題の解き方をわかりやすく


曲率半径



中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
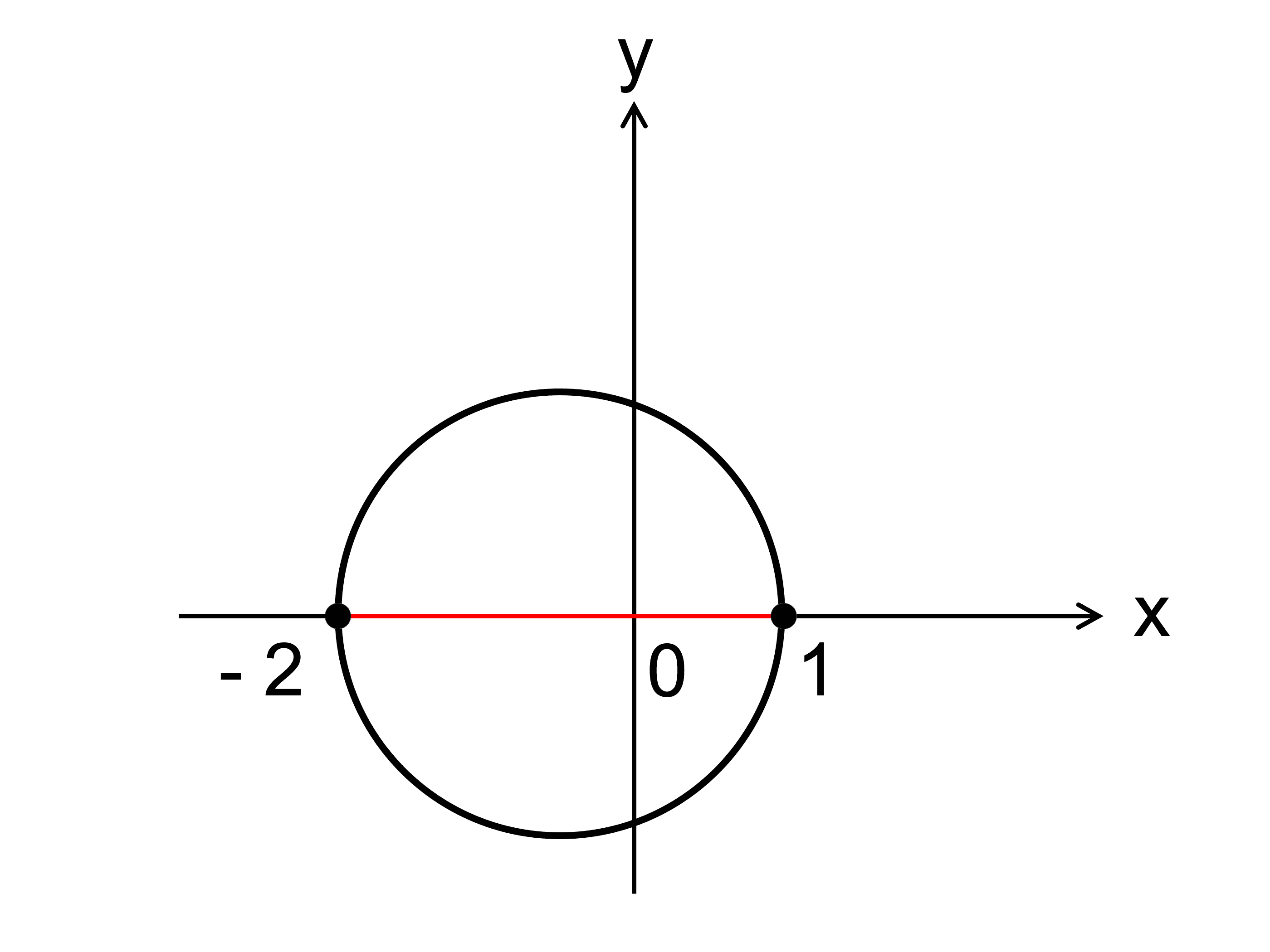


円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



3点を通る円 の作図方法 コンパス 定規 数学fun



円の中心を求める 3つの方法 Wikihow



円の方程式 数学ii フリー教材開発コミュニティ Ftext


中1 作図 円の中心を求める方法を解説 数スタ



応用 2つの円の交点を通る円や直線 なかけんの数学ノート


平面図形 おうぎ形 4 ネット塾



内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学
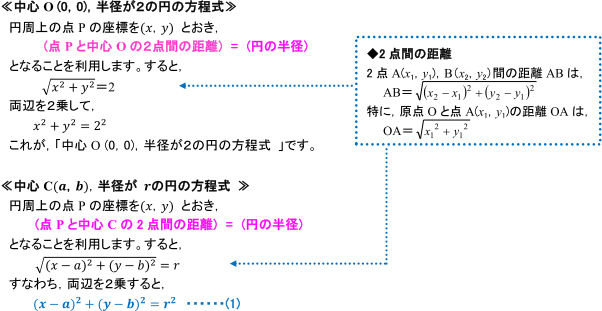


円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション



任意の3点を通る円を求める方法 プログラマーのメモ書き



円 扇形 の面積 周や弧の長さの公式 数学fun


